-
-
Published
Linked with GitHub
# Constant Time Reward Distribution with Changing Stake Sizes and Required Gap
## Introduction
The paper of [Scalable Reward Distribution with Changing Stake Sizes](https://solmaz.io/2019/02/24/scalable-reward-changing/) defines a method to build a pull-based reward system with constant time computation and with the capability of changing the already staked amount. Although these two features are desirable, a participant can still stake just at the moment of the reward distribution, withdrawing the stake just later. This creates an unfair situation where these participants are getting the same reward as other participants that have staked for the complete period duration.
In this paper, we propose an extension to this method to force a fair reward, while keeping the core features. In our solution, the participants are forced to keep the stake during some period, if they want to get the reward. The participants can withdraw their stake at any moment, but if they do, they are not rewarded with the next distributed reward. Their stake needs to be there for at least two distributions, what we call a gap. This incentivizes participants to deposit stake during a complete period, and avoid malicious participants to stake only a small part of the supposed time, behavior that breaks the main purpose of a reward system.
## Features
We call *Gap Reward* to the process of evaluating the reward for a participant only if their stake was there during the last gap, which means: from the previous distribution until the last distribution.
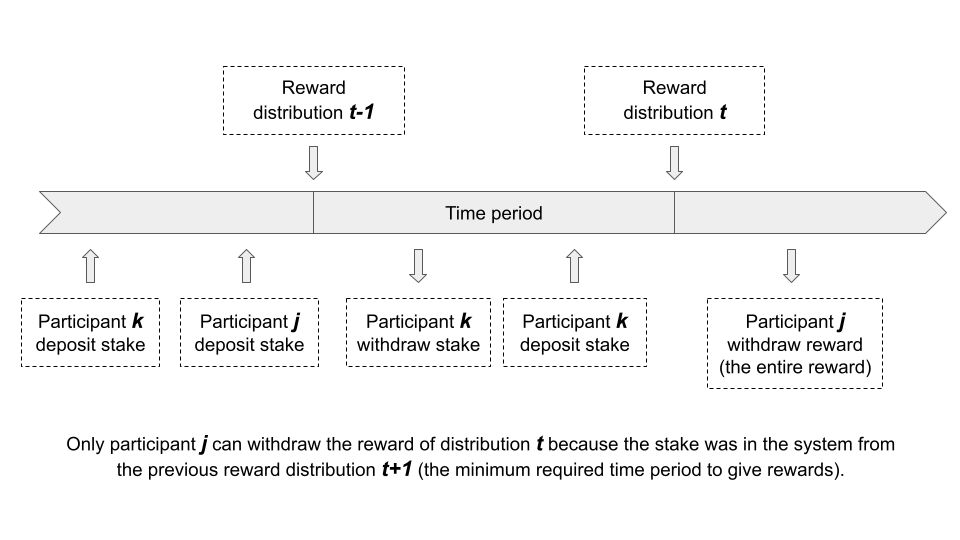
Features of the proposed method are the following:
1. The stake needs to be in the system a required time to be rewarded: minimum a gap.
1. Withdraw stake resets the required time to be rewarded if that stake is deposit again: if a participant withdraw stake and deposit again in the same gap, the new deposited stake still needs to be there for a new gap to be rewarded.
3. The reward given is constant per distribution without loses: if a two participants deposit stake, but one of them withdraws the stake just before finishing the gap, the other participant will get the entire reward.
The cost of adding these features over the original paper method is the addition of a new simple storage to the system. The method remains in constant time computation.
## Methodology
*The reader is supposed to understand the equations of the cited paper in order to follow this explanation. This document will refer to them in several occasions.*
The original paper uses the following reward definition for a participan $j$ that wants to compute the reward given at moment $t$:
$$
reward_{j,t} = stake_{j,t} \frac{reward_{t}}{T_{t}}
$$
In our case, because we want to reward only the stake that has been in the system during at least one interval, the reward given in $t$ only takes into account the previous stake:
$$
reward_{j,t} = stake_{j,t-1} \frac{reward_{t}}{T_{t-1}}
$$
Also, any withdraw stake performed during $t$ could reduce the previous, initially rewarded, $stake_{t-1}$. Our intention is that withdrawals can cancel the previous deposit stake in order to create the required gap. This means that our original value $stake_{t-1}$ can be reduced by withdrawals before reaching the moment $t$ of reward. In the same way, the total previous stake, $T_{t-1}$, must be decreased by the total withdrawal amount, $W_t$, until the moment of reward $t$. This modifies the reward equation as follows:
$$
reward_{j,t} = stake_{j,t-1}' \frac{reward_{t}}{T_{t-1} - W_t}
$$
Where the $stake_{j,t-1}'$ is the previous stake less the total amount of withdrawals done over the previous stake by the participant $j$ in the last gap until the reward $t$, and $W_t$ is the total amount of withdrawals of all participants in that gap:
$$
stake_{j,t-1}' = stake_{j,t-1} - withdrawals_{j, t}
$$
$$
W_t = \sum_{j} withdrawals_{j, t}
$$
Following the same mathematical development of the paper for the original equation, we can now determine the following:
$$
total\_reward_{j,t} = stake_{j,t-1}' \times reward\_per\_token_t - reward\_tally_{j,t}
$$
where:
$$
reward\_per\_token_{t} = \sum_{t=1}^{n} \frac{reward_{t}}{T_{t-1} - W_t}
$$
$$
reward\_tally_{j,t} = \sum_{n=2}^{t} \left( \Delta stake_{j,n-1}' \times reward\_per\_token_{n-1} \right)
$$
From this, we extract that in order to determine the $reward\_per\_token_{n-1}$ value, we need to know before the value of $W_{t-1}$. Nevertheless, this value can vary if a participant action modifies the $\Delta stake_{j,t-1}'$ with a $withdrawals_{j,t}$ value $> 0$, that is, when a participant withdraws stake belonging to the previous distribution $t-1$. This implies that we can not know the correct $reward\_per\_token_{t-1}$ until $t$, because each withdrawal action by any participant can modify it.
This dependency forces us to modify the original method postponing the deposit/withdraw actions until the $t$ reward is given, where we can compute the correct $reward\_per\_token_{t-1}$ having the closed amount $W_{t-1}$ that now remains immutable.
Postponing those actions implies saving in the account the $\Delta stake_{j,t}$ instead of accumulating into the $stake_{j,t}$, and tracking the $t$ where the action happened.
In the next reward distribution event, we can compute the correct $reward\_per\_token_{t-1}$ that should have been used in the deposit/withdraw participant methods. We store that value in pairs $(t, reward\_per\_token_{t})$ accessible for the participant accounts who stored that $t$. This will allow that before computing the reward of an account after a distribution $t$, the $reward_tally_{j,t}$ can be correctly computed using the $reward\_per\_token_{t}$ stored in the new memory of pairs, giving the correct reward.
## Implementation
The following basic Python implementation represents how to implement the *Gap Reward* solution for the same methods found in the paper.
```python
class PullBasedDistribution:
"Constant Time Reward Distribution with Changing Stake Sizes and Required Gap"
def __init__(self):
# Per group
self.total_stake = 0
self.total_pending_stake = 0
self.reward_per_token = 0
self.reward_per_token_history = {}
self.current_distribution_id = 0
# Per account
self.stake = {0x1: 0, 0x2: 0}
self.reward_tally = {0x1: 0, 0x2: 0}
self.pending_stake = {0x1: 0, 0x2: 0}
self.distribution_id = {0x1: 0, 0x2: 0}
def __update_state(self, address):
"Ensure a valid state for the account before using it"
if self.distribution_id[address] != self.current_distribution_id:
self.stake[address] += self.pending_stake[address]
self.reward_tally[address] += (self.pending_stake[address]
* self.reward_per_token_history[self.distribution_id[address]])
self.distribution_id[address] = self.current_distribution_id
self.pending_stake[address] = 0
def distribute(self, reward):
"Distribute `reward` proportionally to active stakes"
if self.total_stake > 0:
self.reward_per_token += reward / self.total_stake
prev_distribution_id = self.current_distribution_id
self.reward_per_token_history[prev_distribution_id] = self.reward_per_token
self.current_distribution_id += 1
self.total_stake += self.total_pending_stake
self.total_pending_stake = 0
def deposit_stake(self, address, amount):
"Increase the stake of `address` by `amount`"
self.__update_state(address)
self.pending_stake[address] += amount
self.total_pending_stake += amount
def withdraw_stake(self, address, amount):
"Decrease the stake of `address` by `amount`"
if amount > self.stake[address] + self.pending_stake[address]:
raise Exception("Requested amount greater than staked amount")
self.__update_state(address)
pending_amount = min(amount, self.pending_stake[address])
self.pending_stake[address] -= pending_amount
self.total_pending_stake -= pending_amount
computed_amount = amount - pending_amount
self.stake[address] -= computed_amount
self.reward_tally[address] -= self.reward_per_token * computed_amount
self.total_stake -= computed_amount
def compute_reward(self, address):
"Compute reward of `address`. Inmutable"
stake = self.stake[address]
reward_tally = self.reward_tally[address]
if self.distribution_id[address] != self.current_distribution_id:
stake += self.pending_stake[address]
reward_tally += self.pending_stake[address] * self.reward_per_token_history[self.distribution_id[address]]
return stake * self.reward_per_token - reward_tally
def withdraw_reward(self, address):
"Withdraw rewards of `address`"
self.__update_state(address)
reward = self.compute_reward(address)
self.reward_tally[address] = self.stake[address] * self.reward_per_token
return reward
# Example
addr1 = 0x1
addr2 = 0x2
contract = PullBasedDistribution()
contract.deposit_stake(addr1, 100)
contract.deposit_stake(addr2, 50)
contract.distribute(0) # Still nothing to reward here
contract.withdraw_stake(addr1, 100)
contract.deposit_stake(addr1, 50)
contract.distribute(10)
# Expected to not be rewarded because the participant withdrawed stake before the second distribution (0)
print(contract.withdraw_reward(addr1))
# Expected to be rewarded with the entire first reward distribution (10)
print(contract.withdraw_reward(addr2))
```
## Conclusion
The original paper gives two important features for a reward system: constant time computation and stake size changes. With two more arithmetic values stored by account and a simple storage per system, we are able to add a new desirable feature without losing its initial capabilities: give the reward only if the participant holds the stake during an established period, or gap. This feature is important to incentivize participants to stake during the time and to avoid malicious behaviors of participants that stake only during the moment the reward is given in the system.
## References
- [Scalable Reward Distribution](http://batog.info/papers/scalable-reward-distribution.pdf): Initial paper where the paper used for this document is based on.
- [Scalable Reward Distribution with Changing Stake Sizes](https://solmaz.io/2019/02/24/scalable-reward-changing/): Paper this document is based on.
- [Scalable Reward Distribution with Changing Stake Sizes and Deferred Reward](https://centrifuge.hackmd.io/@Luis/SkB07jq8o): Sibling method where the reward is deferred to the next distribution. It has the same features except that the reward given in each distribution is not constant. In return, the deferred method does not use an aditional storage.
- [Substrate pallet implementation](https://github.com/centrifuge/centrifuge-chain/tree/main/pallets/rewards/src/mechanism/gap.rs): Rust implementation used in centrifuge.io